已知实数列 等比数列,其中
等比数列,其中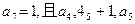 成等差数列.
成等差数列.
(1)求数列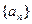 的通项公式;
的通项公式;
(2)数列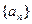 的前
的前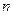 项和记为
项和记为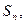 证明:
证明: 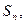 <128
<128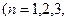 …).
…).
已知矩形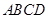 的周长为
的周长为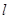 ,面积为
,面积为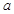 .
.
(1)当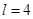 时,求面积
时,求面积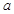 的最大值;
的最大值;
(2)当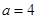 时,求周长
时,求周长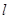 的最小值.
的最小值.
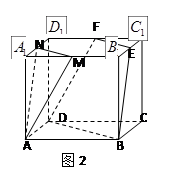
如图2,正方体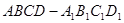 中,
中, 分别是棱
分别是棱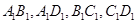 的中点.
的中点.
(1)求证:直线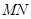 ∥平面
∥平面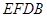 ;
;
(2)求证:平面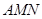 ∥平面
∥平面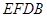 .
.
求满足下列条件的直线的方程.
(1)经过点A(3,2),且与直线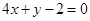 平行;
平行;
(2)经过点B(3,0),且与直线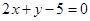 垂直.
垂直.
(1)计算:
(2)计算:
(本小题满分14分)若集合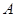 具有以下性质:
具有以下性质:
① ,
, ;
;
②若 ,则
,则 ,且
,且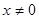 时,
时,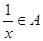 .
.
则称集合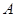 是“好集”.
是“好集”.
(Ⅰ)分别判断集合 ,有理数集
,有理数集 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(Ⅱ)设集合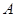 是“好集”,求证:若
是“好集”,求证:若 ,则
,则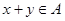 ;
;
(Ⅲ)对任意的一个“好集”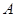 ,
, 分别判断下面命题的真假,并说明理由.
分别判断下面命题的真假,并说明理由.
命题 :若
:若 ,则必有
,则必有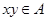 ;
;
命题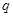 :若
:若
 ,且
,且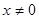 ,则必有
,则必有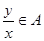 ;
;