如图,为多面体,平面与平面垂直,点在线段上,都是正三角形.
(Ⅰ)证明直线;
(2)求棱锥的体积.

(本小题满分12分)为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
(1)根据二维条形图,完形填空2×2列联表:
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
(本小题满分12分)在平行六面体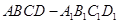 中,
中,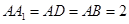 ,
,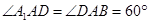 ,
,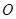 是
是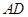 的中点.
的中点.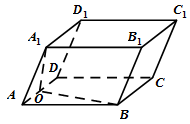
(1)证明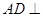 面
面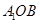 ;
;
(2)当平面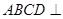 平面
平面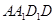 ,求
,求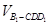 .
.
【改编题】在锐角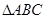 中,
中,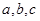 分别为
分别为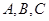 的对边,已知
的对边,已知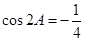 .
.
(1)求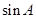 ;
;
(2)当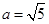 ,求
,求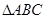 的面积得最大值.
的面积得最大值.
【原创】若数列 的前
的前 项和
项和 ,则()
,则() 是等比数列 B.
是等比数列 B. 是等差数列
是等差数列
C.当 时,
时, 是等比数列 D.当
是等比数列 D.当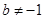 时,
时, 是等比数列
是等比数列
(本小题满分14分)已知函数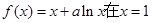 处的切线l与直线
处的切线l与直线 垂直,函数
垂直,函数
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数 存在单调递减区间,求实数
存在单调递减区间,求实数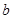 的取值范围;
的取值范围;
(Ⅲ)设 是函数
是函数 的两个极值点,若
的两个极值点,若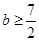 ,求
,求 的最小值.
的最小值.