在数1和100之间插入个实数,使得这个数构成递增的等比数列,将这个数的乘积记作,再令,.
(Ⅰ)求数列的通项公式;
(Ⅱ)设求数列的前项和.
(本题满分14分) 已知函数 ,将函数
,将函数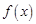 的图像向左平移
的图像向左平移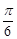 个单位后得函数
个单位后得函数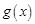 的图像,设
的图像,设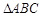 的三个角
的三个角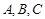 的对边分别为
的对边分别为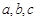 .
.
(Ⅰ)若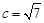 ,
,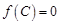 ,
,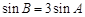 ,求
,求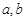 的值;
的值;
(Ⅱ)若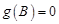 且
且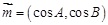 ,
,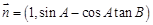 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
已知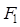 (
(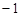 ,0),
,0), (1,0),
(1,0),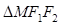 的周长为6.
的周长为6.

(Ⅰ)求动点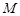 的轨迹
的轨迹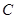 的方程;
的方程;
(II)试确定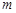 的取值范围,使得轨迹
的取值范围,使得轨迹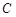 上有不同的两点
上有不同的两点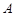 、
、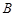 关于直线
关于直线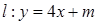 对称.
对称.
.(本小题满分12分)
设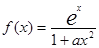 ,其中
,其中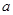 为正实数.
为正实数.
(Ⅰ)当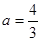 时,求
时,求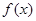 的极值点;
的极值点;
(Ⅱ)若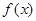 为R上的单调函数,求
为R上的单调函数,求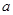 的取值范围.
的取值范围.
(本小题满分12分)
如图,四棱锥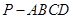 的底面是正方形,
的底面是正方形,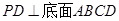 ,点E在棱PB上.
,点E在棱PB上.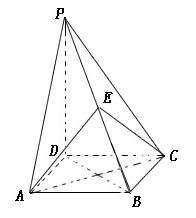
(Ⅰ)求证:PB⊥AC;
(Ⅱ) 当PD=2AB,E在何位置时, PB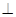 平面EAC;
平面EAC;
(Ⅲ) 在(Ⅰ)的情况下,求二面E-AC-B的余弦值.
(本小题满分12分)
某校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率; (ii)获奖的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望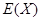 .
.