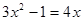已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以
AD为边作菱形ADEF,使∠DAF=60°,连接CF.
⑴如图1,当点D在边BC上时,
求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
⑵如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
⑶如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠A CB、∠DAC之间存在的等量关系.
CB、∠DAC之间存在的等量关系.
将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
已知关于x的方程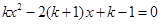 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.
某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30 20 21 20 26 30 25 21 19 28 26
(1)上述数据中,众数是__________万元,中位数是__________万元,平均数是__________万元;
(2)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
(每题4分,共12分)用你喜欢的方法解下列方程:
(1)
(2)
(3)