如图甲所示,相距为L的光滑足够长平行金属导轨水平放置,导轨一部分处在垂直于导轨平面的匀强磁场中,OO′为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距OO′为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。若ab杆在恒力作用下由静止开始向右运动3L的距离,其v-s的关系图象如图乙所示,求:
(1) 在金属杆ab穿过磁场的过程中,通过ab杆的感应电流方向;
(2)金属杆ab离开磁场后的加速度a;
(3)金属杆ab在离开磁场前瞬间的加速度a';
(4)在整个过程中电阻R上产生的电热Q1是多少?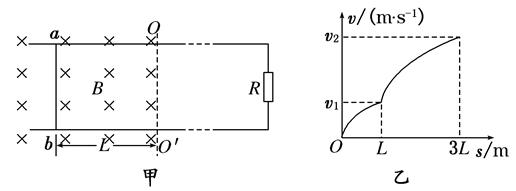
(10分)汤姆孙用来测定电子的比荷(电子的电荷量与质量之比)的实验装置如图所示,真空管内的阴极K发出的电子经加速电压加速后,穿过A’中心的小孔沿中心线(O1O的方向进入到两块水平正对放置的平行极板P和P’间的区域,极板间距为d。当P和P’极板间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;当P和P’极板间加上偏转电压U后,亮点偏离到O’点;此时,在P和P’间的区域,再加上一个方向垂直于纸面向里的匀强磁场,调节磁场的强弱,当磁感应强度的大小为B时,亮点重新回到O点。不计电子的初速度、所受重力和电子间的相互作用。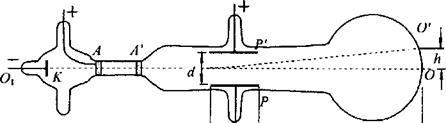
(1)求电子经加速电场加速后的速度大小;
(2)若不知道加速电压值,但己知P和P’极板水平方向的长度为L1,它们的右端到荧光屏中心O点的水平距离为L2,(O于O’点的竖直距离为h,(O'与0点水平距离可忽略不计),求电子的比荷。
如图所示,两根竖直放置的足够长的光滑平行金属导轨间距l=0.50m,上端接有阻值R=0.80Ω的定值电阻,导轨的电阻可忽略不计。导轨处于磁感应强度5=0.40T、方向垂直于金属导轨平面向外的有界匀强磁场中,磁场的上边界如图中虚线所示,虚线下方的磁场范围足够大。一根质量m=4.0x10 2kg、电阻r=0.20Ω的金属杆从距磁场上边界h=0.20m高处,由静止开始沿着金属导轨下落。已知金属杆下落过程中始终与两导轨垂直且接触良好,重力加速度g=10m/S2,不计空气阻力。
(1)求金属杆刚进入磁场时切割磁感线产生的感应电动势大小;
(2)求金属杆刚进入磁场时的加速度大小;
(3)若金属杆进入磁场区域一段时间后开始做匀速直线运动,则金属杆在匀速下落过程中其所受重力对它做功的功率为多大?
一小型交流发电机产生正弦式交变电流,其电压“随时间t变化的规律如图所示。发电机线圈电阻为5Ω,当发电机输出端仅接入一个95Ω的纯电阻用电器时,用电器恰能正常工作。求: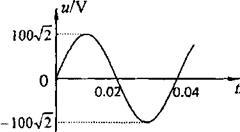
(1)通过该用电器的电流值;
(2)该用电器的额定功率是多少。
甲、乙两物体分别做匀加速和匀减速直线运动,已知乙的初速度是甲的初速度的2.5倍,且甲的加速度大小是乙的加速度大小的2倍,经过4s,两者的速度均达到8m/s,则两者的初速度分别为多大?两者的加速度分别为多大?
如图甲所示为车站使用的水平传送装置的示意图。绷紧的传送带长度L=6.0m,以v=6.0m/s的恒定速率运行,传送带的水平部分AB距离水平地面的高度h=0.45m。现有一行李箱(可视为质点)质量m=10kg,以v0=5.0m/s的水平初速度从A端滑上传送带,被传送到B端时没有被及时取下,行李箱从B端水平抛出,行李箱与传送带间的动摩擦因数μ=0.20,不计空气阻力,重力加速度g取10 m/s2。试分析求解: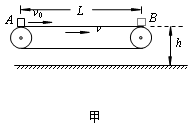
(1)行李箱从传送带上A端运动到B端过程中摩擦力对行李箱冲量的大小;
(2)为运送该行李箱电动机多消耗的电能;
(3)若传送带的速度v可在0~8.0m/s之间调节,仍以v0的水平初速度从A端滑上传送带,且行李箱滑到B端均能水平抛出。请你在图乙中作出行李箱从B端水平抛出到落地点的水平距离x与传送带速度v的关系图象。(要求写出作图数据的分析过程)