某品牌电视生产厂家有 、
、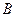 两种型号的电视参加了家电下乡活动,若厂家对
两种型号的电视参加了家电下乡活动,若厂家对 、
、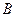 两种型号电视机的投放金额分别为
两种型号电视机的投放金额分别为 、
、 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为 、
、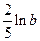 万元,已知
万元,已知 、
、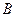 两种型号电视机的投放总金额为10万元,且
两种型号电视机的投放总金额为10万元,且 、
、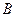 两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为
两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为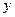 万元,写出
万元,写出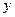 与
与 的函数关系式,并求补贴最多的方案.(精确到
的函数关系式,并求补贴最多的方案.(精确到 ,参考数据:
,参考数据: )
)
某公司计划2015年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元,问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?
(1)解关于 不等式
不等式 .
.
(2)证明: (其中
(其中 ).
).
已知等差数列 的前n项和为
的前n项和为 ,且
,且 ,
,
(1)求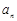 ;
;
(2)求 的最大值.
的最大值.
设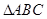 的三边长分别为
的三边长分别为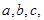 已知
已知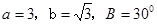 .
.
(1)求A;
(2)求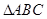 的面积S.
的面积S.
已知抛物线 :
: ,过点
,过点 的直线
的直线 交抛物线
交抛物线 于
于 ,
,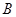 两点.
两点.
(1)若抛物线 的焦点为
的焦点为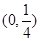 ,求该抛物线的方程;
,求该抛物线的方程;
(2)已知过点 ,
,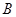 分别作抛物线
分别作抛物线 的切线
的切线 ,
,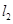 ,交于点
,交于点 ,以线段
,以线段 为直径的圆经过点
为直径的圆经过点 ,求实数
,求实数 的值.
的值.