在直角坐标系
中，以原点
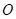为极点，以
轴非负半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系．设曲线
参数方程为
（
为参数），直线
的极坐标方程为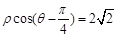
.
（1）写出曲线的普通方程和直线的直角坐标方程；
（2）求曲线上的点到直线的最大距离.
近年来，我国机动车拥有量呈现快速增加的趋势，可与之配套的基础设施建设速度相对迟缓，交通拥堵问题已经成为制约城市发展的重要因素，为了解某市的交通状况，现对其6条道路进行评估，得分分别为5、6、7、8、9、10规定评估的平均得分与全市的总体交通状况等级如下表：
| 评估的平均得分 |
[0，6] |
[6，8] |
[8，10] |
| 全市的总体交通 |
不合格 |
合格 |
优秀 |
（1）求本次评估的平均得分，并参照上表估计该市的总体交通状况等级。
（2）用简单随机抽样方法从6条道路中抽取2条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过0.5的概率
已知△ABC的周长为
，且
，角A、B、C所对的边为a、b、c（1）求AB的长；（2）若△ABC的面积为
求角C的大小。
已知抛物线
和直线
没有公共点（其中
、
为常数），动点
是直线
上的任意一点，过点引抛物线
的两条切线，切点分别为
、
，且直线
恒过点
.
（1）求抛物线的方程；
（2）已知
点为原点，连结
交抛物线于
、
两点，证明：
.
已知函数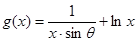
在[1，＋∞）上为增函数，且
，
，
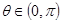∈R．
（1）求θ的值；
（2）若
在[1，＋∞）上为单调函数，求m的取值范围；
（3）设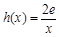
，若在[1，e]上至少存在一个
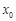，使得
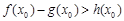成立，求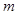
的取值范围．
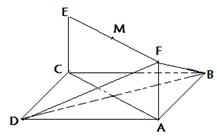
如图示，已知平行四边形ABCD和矩形ACEF所在平面互相垂直，AB=1，AD=2，
是线段EF的中点．
（1）求证：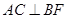
；
（2）设二面角A—FD—B的大小为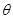
，求
的值；
（3）设点P为一动点，若点P从M出发，沿棱按照
的路线运动到点C，求这一过程中形成的三棱锥P—BFD的体积的最小值．