使得函数值为零的自变量的值称为函数的零点。例如,对于函数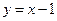 ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数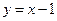 的零点。
的零点。
己知函数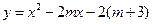 (
(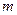 m为常数)。
m为常数)。
(1)当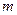 =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论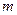 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为 和
和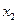 ,且
,且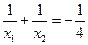 ,此时函数图象与x轴的交点分
,此时函数图象与x轴的交点分
别为A、B(点A在点B左侧),点M在直线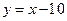 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
(2011贵州黔南,21,10分)为了美化都匀市环境,打造中国优秀旅游城市,现欲将剑江河进行清淤疏通改造,现有两家清淤公司可供选择,这两家公司提供信息如表所示:
| 单位 |
清淤费用(元/m3) |
清淤处理费(元) |
| 甲公司 |
18 |
5000 |
| 乙公司 |
20 |
0 |
(1)若剑江河首批需要清除的淤泥面积大约为1.2万平方米,平均厚度约为0.4米,那么请哪个清淤公司进行清淤费用较省,请说明理由。(体积可按面积×高进行计算)
(2)若甲公司单独做了2天,乙公司单独做了3天,恰好完成全部清淤任务的一半;若甲公司先做2天,剩下的清淤工作由乙公司单独完成,则乙公司所用时间恰好比甲公司单独完成清淤任务所用时间多1天,则甲、乙两公司单独完成清淤任务各需多少时间。
张家界市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
为了建设社会主义新农村,华新村修筑了一条长3000m公路,实际工作效率比原计划提高20%,结果提高前5天完成任务.问原计划每天应修路多长?
某商店第一次用3000元购进某款书包,很快卖完,第二次又用2400元购进该款书包,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个.
(1)求第一次每个书包的进价是多少元?
(2)若第二次进货后按80元/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包按同一标准一次性打折销售,但要求这次的利润不少于480元,问最低可打几折?
徐州至上海的铁路里程为650km。从徐州乘“G”字头列车A、“D” 字头列车B都可直达上海,已知A车的平均速度为B车的2倍,且行驶的时间比B车少2.5h.
(1)设B车的平均速度为x kn/h,根据题意,可列分式方程: ▲;
(2)求A车的平均速度及行驶时间.