(2011贵州黔南,21,10分)为了美化都匀市环境,打造中国优秀旅游城市,现欲将剑江河进行清淤疏通改造,现有两家清淤公司可供选择,这两家公司提供信息如表所示:
| 单位 |
清淤费用(元/m3) |
清淤处理费(元) |
| 甲公司 |
18 |
5000 |
| 乙公司 |
20 |
0 |
(1)若剑江河首批需要清除的淤泥面积大约为1.2万平方米,平均厚度约为0.4米,那么请哪个清淤公司进行清淤费用较省,请说明理由。(体积可按面积×高进行计算)
(2)若甲公司单独做了2天,乙公司单独做了3天,恰好完成全部清淤任务的一半;若甲公司先做2天,剩下的清淤工作由乙公司单独完成,则乙公司所用时间恰好比甲公司单独完成清淤任务所用时间多1天,则甲、乙两公司单独完成清淤任务各需多少时间。
先化简再求值: ,其中
,其中 。
。
解下列方程:(1) ;(2)
;(2)
计算:(1)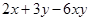 与
与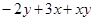 的和;
的和;
化简多项式: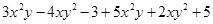

有一些相同的房间需要粉刷墙面,一天3名师傅去粉刷8个房间,结果其中有40㎡墙面未来得及刷;同样时间内5名徒弟粉刷了9个房间的墙面,每名师傅比徒弟一天多刷30㎡墙面.
(1)求每个房间需要粉刷的墙面面积;
(2)张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需几天完成?
(3)已知每名师傅、徒弟每天的工资分别是85元、65元,张老板要求在3天内(包括3天)完成36个房间的粉刷,问如何在这8人中雇用人员(不一定8人全部雇用),才合算呢?
先阅读,后答题。
解方程: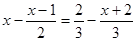
解:去分母,得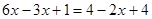 ①
①
即 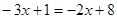 ②
②
移项,得 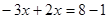 ③
③
合并同类项,得 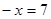 ④
④
∴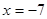 ⑤
⑤
上述解方程的过程中是否有错误?答:_____。
如果有错误,则错在_______步(填相应的序号)。
如果上述解方程有错误,请你给出正确的解题过程: