(本小题满分12分)
已知3名志愿者在10月1号至10月5号期间参加2011年国庆节志愿者活动工作.
(1)若每名志愿者在5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志原者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量 的数学期望.
的数学期望.
(理科)已知抛物线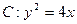 的准线与
的准线与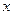 轴交于
轴交于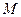 点,
点, 为抛物线
为抛物线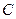 的焦点,过
的焦点,过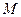 点斜率为
点斜率为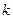 的直线与抛物线
的直线与抛物线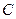 交于
交于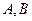 两点。
两点。
(1)若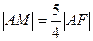 ,求
,求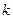 的值;
的值;
(2)是否存在这样的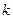 ,使得抛物线
,使得抛物线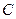 上总存在点
上总存在点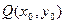 满足
满足 ,若存在,求
,若存在,求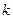 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
某车间共有12名工人,需配备两种型号的机器,每台A型机器需2人操作,每天耗电30千瓦时,能生产出价值4万元的产品;每台B型机器需3人操作,每天耗电20千瓦时,能生产出价值3万元的产品,现每天供应车间的电量不多于130千瓦时,问这个车间如何配备这两种型号的机器,使每天的产值最大?最大产值是多少万元?
已知直线 与圆
与圆 相交于
相交于 两点,
两点, 是坐标原点,三角形
是坐标原点,三角形 的面积为
的面积为 。
。
(1)试将 表示成
表示成 的函数,并求出它的定义域;
的函数,并求出它的定义域;
(2)求 的最大值,并求取得最大值时
的最大值,并求取得最大值时 的值。
的值。
光线自点 射入,经直线
射入,经直线 反射后经过点
反射后经过点 ,求反射光线所在的直线方程。
,求反射光线所在的直线方程。
已知 .
.
(1)求函数 的定义域;
的定义域;
(2)判断并用定义证明函数 的单调性;
的单调性;
(3)求函数 的反函数.
的反函数.