△ABC是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2，
（1）要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1），比较甲、乙两种剪法，哪种剪法所得的正方形面积大？请说明理由．
（2）图1中甲种剪法称为第1次剪取，记所得正方形面积为s1；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为s2（如图2），则s2=
；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为s3，继续操作下去…，则第10次剪取时，s10=
；
（3）求第10次剪取后，余下的所有小三角形的面积之和．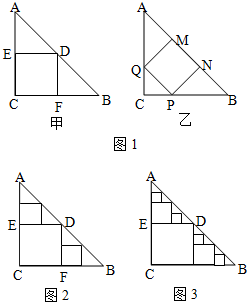
(本题10分)已知，如图，△OAB中，OA=OB，⊙O经过AB的中点C，且与OA、OB分别交于点D、E. (1) 如图①，判断直线AB与⊙O的位置关系并说明理由；
(2) 如图②，连接CD、CE，当△OAB满足什么条件时，四边形ODCE为菱形，并证明你的结论。
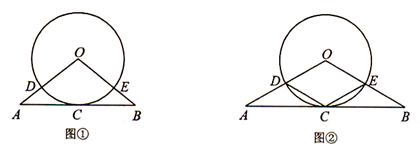
(本题10分)经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转.如果这三种可能性大小相同，现有两辆汽车经过这个十字路口.(1) 试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果；
(2) 求至少有一辆汽车向左转的概率.
如图，点A、O、B在同一条直线上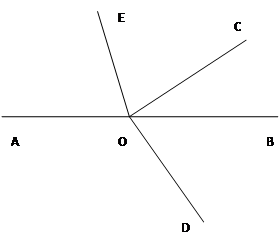
（1）∠AOC比∠BOC大100°，求∠AOC与∠BOC的度数
（2）在(1)的条件下，若∠BOC与∠BOD互余，求∠BOD的度数
（3）在（2）的条件下，若OE平分∠AOC，求∠DOE的度数
．(本题8分)如图，在正方形ABCD中，E为对角线AC上一点，连接EB、ED．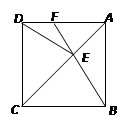
(1) 写出图中所有的全等三角形
(2) 延长BE交AD于点F，若∠DEB ＝ 140°，求∠AFE的度数．
(本题8分) 先将
÷
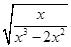化简，然后自选一个合适的x值，代入化简后的式子求值。