某工厂生产一种产品的成本费用由三部分组成：①职工工资固定支出12500元；②原材料费每件40元；③电力与机器保养费用为每件0.05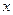
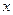元，其中是该厂生产这种产品的总件数。
（1）求生产每件产品的职工工资固定支出的费用
(元);
（2）把每件产品的成本费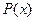
（元）表示成产品件数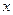的函数，并求生产每件这种产品的成本费的最小值；
（3）如果该厂生产的这种产品的数量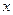不超过3000件，且产品能全部销售。根据市场调查：每件产品的销售价
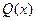与产品件数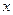有如下的关系：
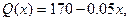试问生产多少件产品，总利润最高？
（总利润=总销售额—总的成本）
（本小题满分12分）
在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人。女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个2×2列联表；
（2）判断休闲方式与性别是否有关。
（参考公式：
参考数据：
）
（本小题满分12分）
有20件产品，其中5件是次品，其余都是合格品，现不放回的从中依次抽2件，求：
（
1）第一次抽到次品的概率；
（2）第一次和第二次都抽到次品的概率；
（3）在第一次抽到次品的条件下，第二次抽到次品的概率。
已知函数
在
处切线斜率为-1.
(I)求
的解析式；
（Ⅱ）设函数
的定义域为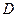
，若存在区间
，使得在
上的值域也是，则称区间为函数的“保值区间”
（ⅰ）证明：当
时，函数不存在“保值区间”；
（ⅱ）函数是否存在“保值区间”？若存在，写出一个“保值区间”（不必证明）；若不存在，说明理由.
已知函数
的极大值点为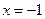
，
（1）用实数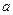
来表示
实数
，并求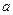的取值范围；
（2）当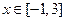
时，若
的最大值为6，求实数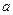的值.
某品牌电视生产厂家有
、
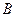两种型号的电视参加了家电下乡活动，若厂家对、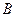两种型号电视机的投放金额分别为
、
万元，农民购买电视机获得的补贴分别为
、
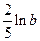万元，已知、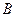两种型号电视机的投放总金额为10万元，且、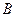两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为
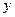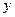万元，写出与的函数关系式，并求补贴最多的方案.（精确到
，参考数据：
）