用144分米长的铁丝围成一个长方体框架，一只蚂蚁从顶点A出发-优题课

用144分米长的铁丝围成一个长方体框架，一只蚂蚁从顶点A出发，沿棱爬行，经顶点BC到达D，已知蚂蚁每分钟爬行6分米经BC比AB多用1分钟，经CD比BC少用2分钟，这个长方体框架的长宽高各是多少？

科目数学题型解答题难度中等

解方程
（1）3（y+1）=2y﹣1
（2）2﹣=．

（1）先化简，再求值： $x^{2} + 2 x - 3 (x^{2} - \frac{2}{3} x)$ ，其中 $x = - \frac{1}{2}$ ．

（2）计算： $\frac{1}{2} x y - 2 (x y - \frac{1}{3} x y^{2}) + (\frac{3}{2} x y + \frac{1}{3} x y^{2})$ ，其中 $x$ 、 $y$ 满足 $| x - 6 | + (y + 2)^{2} = 0$ ．

如图，已知O为直线AD上一点，射线OC，射线OB，∠AOC与∠AOB互补，OM，ON分别为∠AOC，∠AOB的平分线，若∠MON=40°．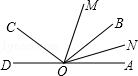

（1）∠COD与∠AOB相等吗？请说明理由；
（2）试求∠AOC与∠AOB的度数．

某礼品制造工厂接受一批玩具的订货任务，按计划天数生产，如果每天生产20个玩具，则比订货任务少100个；如果每天生产23个玩具，则可以超过订货任务20个．请求出这批玩具的订货任务是多少个？原计划几天完成任务？

如图，直线AB和EF相交于O，OC平分∠AOB，∠1=65°，试求∠3的度数．