(本题10分) 在一个盒中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,求(Ⅰ)从中任取1枝,得到一等品或二等品的概率;
(Ⅱ)从中任取2枝,没有三等品的概率.
(本小题满分12分) 如图,已知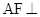 平面
平面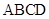 ,四边形
,四边形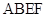 为矩形,四边形
为矩形,四边形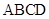 为直角梯形,
为直角梯形,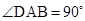 ,
,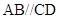 ,
,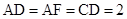 ,
,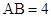 .
.
(Ⅰ)求证: 平面
平面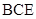 ;
;
(Ⅱ)求三棱锥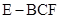 的体积.
的体积.
(本小题满分12分)为了解惠州市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10。规定评估的平均得分与全市的总体交通状况等级如下表:
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;
(2)用简单随机抽样方法从这 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体
条,它们的得分组成一个样本,求该样本的平均数与总体
的平均数之差的绝对值不超过 的概率.
的概率.
(本小题满分10分)选修4-5:不等式选讲
设函数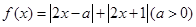 ,
, .
.
(Ⅰ)当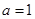 时,求不等式
时,求不等式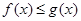 的解集;
的解集;
(Ⅱ)若 恒成立,求实数
恒成立,求实数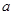 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系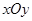 中,直线
中,直线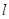 的参数方程
的参数方程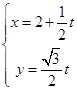 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,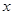 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线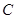 的极坐标方程为:
的极坐标方程为: .
.
(Ⅰ)求直线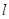 的极坐标方程;
的极坐标方程;
(Ⅱ)求直线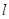 与曲线
与曲线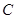 交点的极坐标
交点的极坐标 .
.
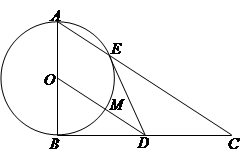
(本小题满分10分)选修4-1:几何证明选讲
如图,在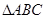 中,
中,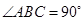 ,以
,以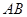 为直径的圆
为直径的圆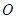 交
交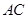 于点
于点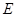 ,点
,点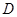 是
是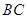 边的中点,连接
边的中点,连接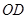 交圆
交圆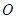 于点
于点 .
.
(Ⅰ)求证: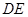 是圆
是圆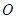 的切线;
的切线;
(Ⅱ)求证: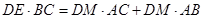 .
.