(本题11分)在△ABC中,角A、B、C的对边分别为 、
、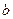 、
、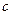 ,且
,且
(1)判断△ABC的形状;
(2)设向量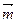 =(2
=(2 ,
,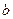 ) ,
) ,  =(
=( ,-3
,-3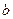 )且
)且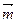 ⊥
⊥ ,(
,(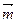 +
+ )(
)( -
-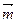 )=14,
)=14,
求S△ABC的值。
如图,三角形 和梯形
和梯形 所在的平面互相垂直,
所在的平面互相垂直,  ,
, ,
, 是线段
是线段 上一点,
上一点, .
.
(Ⅰ)当 时,求证:
时,求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)是否存在点 满足
满足 平面
平面 ?并说明理由.
?并说明理由.
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(I)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量 的分布列和数学期望.
的分布列和数学期望.
在△ABC中,已知A= ,
, .
.
(I)求cosC的值;
(Ⅱ)若BC=2 ,D为AB的中点,求CD的长.
,D为AB的中点,求CD的长.
(本大题满分12分)设函数 (
( 为自然对数的底数),
为自然对数的底数),
(1)当 =1时,求过点(1,
=1时,求过点(1, )处的切线与坐标轴围成的面积;
)处的切线与坐标轴围成的面积;
(2)若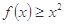 在(0,1)恒成立,求实数
在(0,1)恒成立,求实数 的取值范围.
的取值范围.
(本小题12分)已知 分别为椭圆
分别为椭圆 :
: (
( )的左、右焦点, 且离心率为
)的左、右焦点, 且离心率为 ,点
,点 椭圆
椭圆 上
上
(1)求椭圆 的方程;
的方程;
(2)是否存在斜率为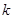 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点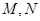 ,使直线
,使直线 与
与 的倾斜角互补,且直线
的倾斜角互补,且直线 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.