(本小题满分10分)选修4—5:不等式选讲。设正有理数 是
是 的一个近似值,令
的一个近似值,令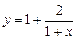 .
.
(Ⅰ)若 ,求证:
,求证:
 ;
;
(Ⅱ)求证: 比
比 更接近于
更接近于 .
.
测量知某班10名男同学身高(单位:cm)如下表
(为方便叙述,将10名同学编号为:0,1,2,3,4,5,6,7,8,9)
| 编号 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 身高 |
1.81 |
1.79 |
1.79 |
1.81 |
1.79 |
1.81 |
1.77 |
1.76 |
1.83 |
1.77 |
其中身高在区间【1.78,1.82】内的同学可以参加升旗仪仗队,
(1)从上述10名同学中,随机抽取1名,求这名同学能参加仪仗队的概率;
(2)从能参加仪仗队的同学中随机抽取2名,
1用同学的编号列出所有可能的抽取结果;
2求这两名同学身高相等的概率
根据下面的程序,画出其相应的程序框图,并说明此题所表述算法的功能。
)某次考试结束后,学校从参加检测的高一学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中的平均分;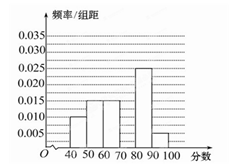
如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.
⑴求证:平面ABM⊥平面PCD;
⑵求直线PC与平面ABM所成角的正切值;
⑶求点O到平面ABM的距离.
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF//AC,AB= ,
,
CE=EF=1
⑴求证:AF//平面BDE
⑵求证:CF⊥平面BDE