某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一类),并根据调查结果制作了尚不完整的频数分布表:
| 类别 |
频数(人数) |
频率 |
| 文学 |
m |
0.42 |
| 艺术 |
22 |
0.11 |
| 科普 |
66 |
n |
| 其他 |
28 |
|
| 合计 |
|
1 |
(1)表中m=_______,n=________;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最多?最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普类读物的学生有多少人?
(1)解方程:
①x2-6x-4=0
②x2-12x+27=0
(2)直接写出方程(x2-6x-4)(x2-12x+27)=0的解为 .
为了节约用水,某市规定三口之家每月标准用水量为15立方米,超过部分加价收费,假设不超过部分水费为1.5元/立方米,超过部分水费为3元/立方米。
(1)当每月用水量为a立方米时,请用代数式分别表示这家按标准用水量和超出标准用水时各应缴纳的水费;
(2)如果甲、乙两家用水量分别为10立方米和20立方米,那么甲、乙两家该月应各交多少水费?
(3)当丁家本月交水费46.5元时,那么丁家该月用水多少立方米?
已知DB∥FG ∥EC,∠ABD=84°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数。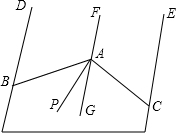
如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数(填理由或数学式)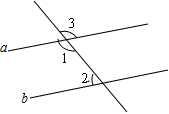
解:∵∠3=131°()
又∵ ∠3=∠1()
∴ ∠1=()()
∵ a∥b()
∴ ∠1+∠2=180°()
∴ ∠2=()()
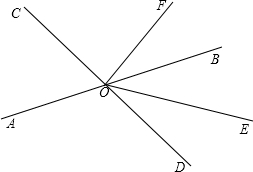
如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,OF⊥CD,垂足为O,求∠EOF的度数。