如图,现在要在一块半径为1m。圆心角为60°的扇形纸板AOB上剪出一个平行
四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设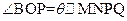 的
的
面积为S。
(1)求S关于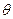 的函数
的函数 关系式;
关系式;
(2)求S的最大值及相应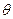 的值
的值
(本小题满分12分)设数列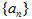 的前
的前 项和
项和 满足:
满足: ,等比数列
,等比数列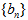 的前
的前 项和为
项和为 ,公比为
,公比为 ,且
,且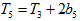 .
.
(1)求数列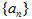 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为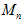 ,求证:
,求证: .
.
(本小题满分10分)
已知函数 ,
,
(1)若关于 的方程
的方程 只有一个实数解,求实数
只有一个实数解,求实数 的取值范围;
的取值范围;
(2)若当 时,不等式
时,不等式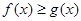 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若 ,求函数
,求函数 在区间
在区间 上的最大值.
上的最大值.
(本小题满分8分)
已知幂函数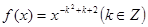 ,且
,且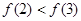 。
。
(1)求 的值;
的值;
(2)试判断是否存在正数 ,使函数
,使函数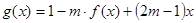 在区间
在区间 上的值域为
上的值域为 ,若存在求出
,若存在求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(本小题满分10分)已知函数
 (
( 是常数),且
是常数),且 ,
, .
.
(1)求 的值;
的值;
(2)当 时,判断
时,判断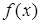 的单调性并证明;
的单调性并证明;
(3)若不等式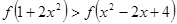 成立,求实数
成立,求实数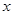 的取值范围.
的取值范围.
(本小题满分8分)
已知函数
(1) 若函数 的图象经过点
的图象经过点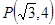 ,求
,求 的值;
的值;
(2) 判断并证明函数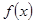 的奇偶性;
的奇偶性;
(3) 比较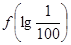 与
与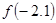 的大小,并写出必要的理由.
的大小,并写出必要的理由.