(本小题满分10分)(选修4-1:几何证明选讲)
如图: 是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。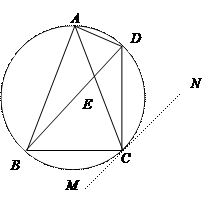
(1)求证: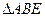

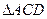 ;
;
(2)若AB=6,BC=4,求AE。
(本小题满分12分)已知函数 ,
, .
.
(1)若函数 是单调递增函数,求实数
是单调递增函数,求实数 的取值范围;
的取值范围;
(2)当 时,两曲线
时,两曲线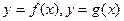 有公共点P,设曲线
有公共点P,设曲线 在P处的切线分别为
在P处的切线分别为 ,若切线
,若切线 与
与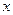 轴围成一个等腰三角形,求P点坐标和
轴围成一个等腰三角形,求P点坐标和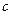 的值;
的值;
(3)当 时,讨论关于
时,讨论关于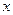 的方程
的方程 的根的个数。
的根的个数。
(本小题满分12分)设A、B分别是 轴,
轴,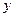 轴上的动点,P在直线AB上,且
轴上的动点,P在直线AB上,且
(1)求点P的轨迹E的方程;
(2)已知E上定点K(-2,0)及动点M、N满足 ,试证:直线MN必过
,试证:直线MN必过 轴上的定点。
轴上的定点。
(本小题满分12分)
(1)连续抛掷两枚正方体的骰子(它们的六个面分别标有数字1,2,3,4,5,6),记所得朝上的面的点数分别为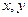 ,过坐标原点和点P(
,过坐标原点和点P(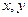 )的直线的倾斜角为
)的直线的倾斜角为  ,求
,求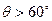 的概率;
的概率;
(2)若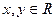 ,且
,且 ,过坐标原点和点P(
,过坐标原点和点P(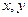 )的直线的斜率为
)的直线的斜率为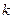 ,求
,求 的概率。
的概率。
(本小题满分12分)如图,已知三棱锥 ,
,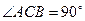 ,
,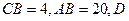 为
为 中点,
中点, 为
为 中点,且
中点,且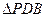 是正三角形,
是正三角形, .
.
(1)求证:平面
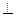 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.