.以下是粤西地区某县搜集到的新房屋的销售价格 和
和 房屋的面积
房屋的面积 的数据:
的数据:
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为 时的销售价格。
时的销售价格。
参考公式:  ,
,
参考数据: ,
,
 ,
,
.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P—EFGH,下半部分是长方体ABCD—EFGH,图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG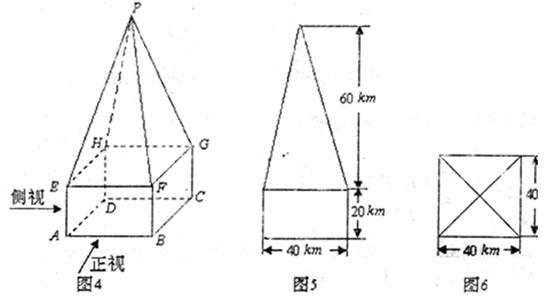
.已知函数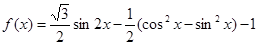
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a,b,c,且c=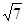 ,
,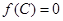 ,若向量
,若向量 共线,求a , b的值。
共线,求a , b的值。
(本小题满分l2分)(注意:在试题卷上作答无效)
已知函数f(x)=x3+bx2+ax+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
(本小题满分l2分)(注意:在试题卷上作答无效)
已知: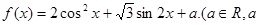 为常数)
为常数)
(I)若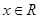 ,求
,求 的最小正周期;
的最小正周期;
(Ⅱ)若 在x∈
在x∈ 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求 的值;
的值;
(Ⅲ)在(2)条件下 先按
先按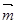 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到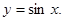 求
求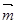 .
.
(本小题满分l2分)(注意:在试题卷上作答无效)
求经过A(2,-1),和直线x+y=1相切,且圆心在直线y=-2x上的圆的方程
(I)求出圆的标准方程
(II)求出(I)中的圆与直线3x+4y=0相交的弦长AB