(本小题满分l2分)(注意:在试题卷上作答无效)
已知: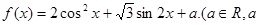 为常数)
为常数)
(I)若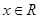 ,求
,求 的最小正周期;
的最小正周期;
(Ⅱ)若 在x∈
在x∈ 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求 的值;
的值;
(Ⅲ)在(2)条件下 先按
先按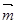 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到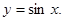 求
求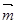 .
.
如图,PA垂直于矩形ABCD所在的平面,PD=PA,E、F分别是AB、PD的中点。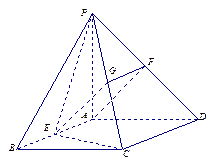
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD。
已知⊿ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:(1) 2sinBcosC-sin(B-C)的值;
(2)若a=2,求⊿ABC周长的最大值。
水库的蓄水量随时间而变化,现用t表示时间(单位:月),以年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为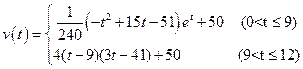 。
。
(1)若该水库的蓄水量小于50的时期称为枯水期,以i-1<t≤i表示第i月份(i=1,2,…12),问一年内那几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取e3=20计算)。
口袋中装有质地大小完全的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号。如果两个编号的和为偶数就算甲胜,否则算乙胜。
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由。
(本小题满分12分)
已知单调递增的等比数列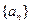 满足:
满足: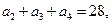 且
且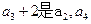 的等差中项。
的等差中项。
(I)求数列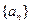 的通项公式;
的通项公式;
(II)设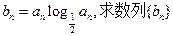 的前n项和
的前n项和