已知函数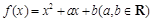 ,
,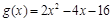 ,且
,且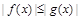 对
对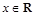 恒成立.
恒成立.
(1)求a、b的值;
(2)若对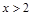 ,不等式
,不等式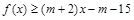 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)记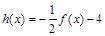 ,那么当
,那么当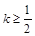 时,是否存在区间
时,是否存在区间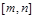 (
(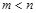 ),使得函数
),使得函数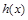 在区间
在区间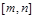 上的值域恰好为
上的值域恰好为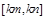 ?若存在,请求出区间
?若存在,请求出区间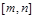 ;若不存在,请说明理由.
;若不存在,请说明理由.
.(1)、求经过直线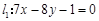 和
和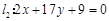 的交点,且垂直于直线
的交点,且垂直于直线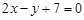 的直线方程.(2)、直线l经过点
的直线方程.(2)、直线l经过点 ,且和圆C:
,且和圆C: 相交,截得弦长为
相交,截得弦长为 ,求l的方程.
,求l的方程.
(普通班)如图所示,从椭圆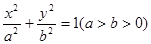 上一点M向
上一点M向 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点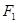 ,且它的长轴端点A及短轴端点B的连线
,且它的长轴端点A及短轴端点B的连线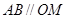 .
.
(1) 求椭圆的离心率e;
(2) 设Q是椭圆上任意一点, 是右焦点,
是右焦点,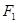 是左焦点,求
是左焦点,求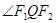 的取值范围;
的取值范围;
(奥班)已知双曲线C: ,
,
(1) 求双曲线C的渐近线方程;
(2) 已知点M的坐标为(0,1).设P是双曲线C上的点,Q是点P关于原点的对称点.记 ,求λ的取值范围;
,求λ的取值范围;
(3) 已知点D、E、M的坐标分别为(-2,-1)、(2,-1)、(0,1),P为双曲线C上在第一象限内的点.记l为经过原点与点P的直线,s为△DEM截直线l所得线段的长.试将s表
示为直线l的斜率k的函数.
椭圆 与直线
与直线 相交于A,B两点,C是AB的中点,若
相交于A,B两点,C是AB的中点,若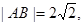 OC的斜率为
OC的斜率为 ,求椭圆的方程。
,求椭圆的方程。
(普通班)设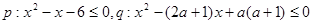 ,若
,若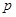 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数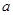 的取值范围。
的取值范围。