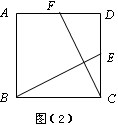
(本题8分)如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连结OA，此时有OA//PE．
（1）求证：AP=AO；
（2）若tan∠OPB=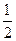
，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ▲ ，能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .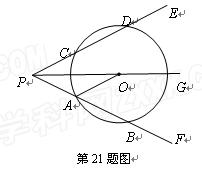
计算：⑴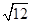
＋(3－π)0－2sin60°⑵
×
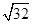＋(－1)2
如图，在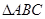
中，AB=AC=10cm， BC=16cm，DE=4cm．线段DE（端点D从点B开始）沿BC边以1cm／s的速度向点C运动，当端点E到达点C时停止运动．过点E作EF∥AC交AB于点F，连接DF，设运动的时间为t秒（t≥0）．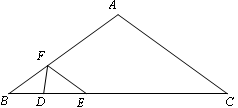
（1）用含t的代数式表示线段EF的长度为；
（2）在运动过程中，△DEF能否为等腰三角形？若能，请求出t的值；若不能，试说明理由．
（3）设M、N分别是DF、EF的中点，请直接写出在整个运动过程中，线段MN所扫过的图形的面积．
销售甲、乙两种商品所得利润分别为y1(万元)和y2(万元)，它们与投入资金u的关系式为y1＝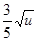
，y2＝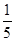
u．如果将3万元资金投入经营甲、乙两种商品，其中对甲商品的投资为x(万元)．
（1）求经营甲、乙两种商品的总利润y（万元）与x的函数关系式，并直接写出自变量x的取值范围；
（2）设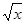
＝t，试写出y关于t的函数关系式，并求出经营甲、乙两种商品各投入多少万元时使得总利润最大．
如图，已知△ABC内接于⊙O，点D在OC的延长线上，∠ABC＝∠CAD.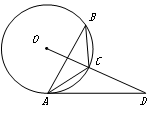
（1）若∠ABC＝20°，则∠OCA的度数为；
（2）判断直线AD与⊙O的位置关系，并说明理由；
（3）若OD⊥AB，BC＝5，AB＝8，求⊙O的半径．
我们学习过：在平面内，将一个图形绕一个定点沿着某个方向转动一个角度，这样的图形运动叫做旋转，这个定点称为旋转中心，旋转的角度称为旋转角．
（1）如图（1），△ABC经过旋转得到△DEF．试用直尺和圆规作出旋转中心 (保留作图痕迹，不写作法) ；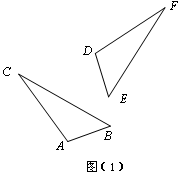
（2）如图（2），正方形ABCD中，E、F分别为CD、AD的中点，连接BE、CF，△BCE按逆时针方向旋转后得到△CDF，则旋转中心为（请在图中画出该点，标上字母，并回答），旋转的最小角度为．