如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠ABC=∠CAD.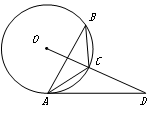
(1)若∠ABC=20°,则∠OCA的度数为 ;
(2)判断直线AD与⊙O的位置关系,并说明理由;
(3)若OD⊥AB,BC=5,AB=8,求⊙O的半径.
如图, 内接于 , ,点 在直径 的延长线上,且 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 ,求阴影部分的面积.
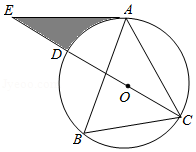
如图, 的对角线 、 相交于点 ,过点 作 ,分别交 、 于点 、 ,连接 、 .
(1)若 ,求 的长;
(2)判断四边形 的形状,并说明理由.

如图,某公司会计欲查询乙商品的进价,发现进货单已被墨水污染.
进货单
|
商品 |
进价(元 件) |
数量(件 |
总金额(元 |
|
甲 |
|
7200 |
|
|
乙 |
3200 |
||
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下:
李阿姨:我记得甲商品进价比乙商品进价每件高 .
王师傅:甲商品比乙商品的数量多40件.
请你求出乙商品的进价,并帮助他们补全进货单.
防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了 、 、 三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.
(1)小明从 测温通道通过的概率是 ;
(2)利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.
扬州教育推出的"智慧学堂"已成为同学们课外学习的得力助手.为了解同学们"智慧学堂"平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图两幅尚不完整的统计图.
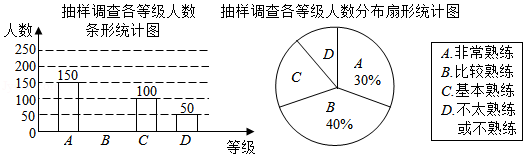
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ,扇形统计图中表示 等级的扇形圆心角为 ;
(2)补全条形统计图;
(3)学校拟对"不太熟练或不熟练"的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.