(本小题满分12分)已知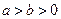 ,证明:
,证明: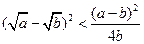 .
.
(本小题满分10分)命题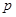 :关于
:关于 的不等式
的不等式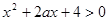 ,对一切
,对一切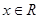 恒成立,命题
恒成立,命题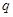 :函数
:函数 是增函数,若
是增函数,若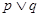 为真,
为真,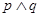 为假,求实数
为假,求实数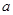 的取值范围.
的取值范围.
已知函数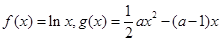 ,(
,(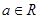 ).
).
(Ⅰ)已知函数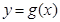 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数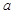 的范围.
的范围.
(Ⅱ)记函数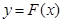 的图象为曲线
的图象为曲线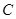 .设点
.设点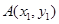 ,
, 是曲线
是曲线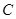 上的不同两点.如果在曲线
上的不同两点.如果在曲线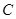 上存在点
上存在点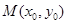 ,使得:①
,使得:① ;②曲线
;②曲线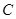 在点
在点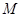 处的切线平行于直线
处的切线平行于直线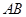 ,则称函数
,则称函数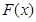 存在“中值相依切线”.
存在“中值相依切线”.
试问:函数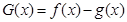 (
(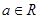 且
且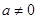 )是否存在“中值相依切线”,请说明理由.
)是否存在“中值相依切线”,请说明理由.
设集合W是满足下列两个条件的无穷数列{an}的集合:①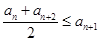 , ②
, ②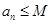 .其中
.其中 ,
, 是与
是与 无关的常数.
无关的常数.
(Ⅰ)若{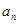 }是等差数列,
}是等差数列,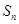 是其前
是其前 项的和,
项的和, ,
,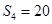 ,证明:
,证明: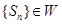 ;
;
(Ⅱ)设数列{ }的通项为
}的通项为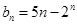 ,且
,且 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设数列{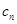 }的各项均为正整数,且
}的各项均为正整数,且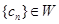 .证明
.证明 .
.
一动圆与圆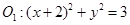 外切,与圆
外切,与圆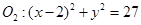 内切.
内切.
(I)求动圆圆心M的轨迹方程.(II)试探究圆心M的轨迹上是否存在点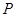 ,使直线
,使直线 与
与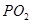 的斜率
的斜率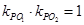 ?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
如图4,已知平面 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线 的中点,已知
的中点,已知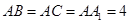
(I))求证: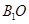 ⊥平面
⊥平面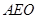 ;
;
(II)求二面角 的余弦值.
的余弦值.
(Ⅲ)求三棱锥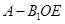 的体积.
的体积. 