解不等式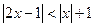
(本题14分)已知不等式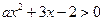 的解集为
的解集为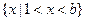 ,
,
(1)求实数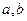 的值;
的值;
(2)解关于 的不等式
的不等式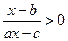 (
( 为实常数)
为实常数)
(本题12分) 若椭圆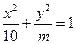 与双曲线
与双曲线 有相同的焦点,且椭圆与双曲线交于点
有相同的焦点,且椭圆与双曲线交于点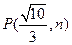 ,求椭圆及双曲线的方程.
,求椭圆及双曲线的方程.
(本题12分)已知命题 ;命题
;命题 表示焦点
表示焦点 轴上的椭圆,若
轴上的椭圆,若 ,求实数
,求实数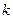 的取值范围.
的取值范围.
(本小题满分10分) 如图,已知椭圆C: ,经过椭圆
,经过椭圆 的右焦点F且斜率为
的右焦点F且斜率为 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在 ,使对任意
,使对任意 ,总有
,总有 成立?若存在,求出所有
成立?若存在,求出所有 的值;
的值;
(II)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本题满分10分)已知双曲线C:
 为C上的任意点.
为C上的任意点.
(Ⅰ)求证:点 到双曲线C的两条渐近线的距离的乘积是一个常数;
到双曲线C的两条渐近线的距离的乘积是一个常数;
(Ⅱ)设点A的坐标为(3,0),求 的最小值.
的最小值.