(本小题满分10分) 如图,已知椭圆C: ,经过椭圆
,经过椭圆 的右焦点F且斜率为
的右焦点F且斜率为 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在 ,使对任意
,使对任意 ,总有
,总有 成立?若存在,求出所有
成立?若存在,求出所有 的值;
的值;
(II)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
如图,已知直线 与抛物线
与抛物线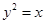 相交于
相交于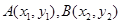 两点,
两点,
与 轴相交于点
轴相交于点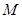 ,若
,若 .
.
(1)求证: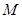 点的坐标为(1,0);
点的坐标为(1,0);
(2)求△AOB的面积的最小值.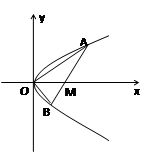
(本小题满分12分)某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.同时,公司每年需要付出设备的维修和工人工资等费用,第一年各种费用2万元,第二年各种费用4万元,以后每年各种费用都增加2万元.
(1)引进这种设备后,第几年后该公司开始获利;
(2)这种设备使用多少年,该公司的年平均获利最大?
(本小题满分12分)
已知双曲线的方程为5x2-4y2=20,左右焦点分别为F1,F2
(1)求此双曲线的焦点坐标和渐近线方程;
(2)若椭圆与此双曲线有共同的焦点,且有一公共点P满足|PF1|·|PF2|=6,求椭圆的标准方程.
(本小题满分12分)等比数列{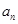 }的前n 项和为
}的前n 项和为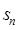 ,已知
,已知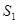 ,
,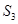 ,
,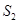 成等差数列.
成等差数列.
(1)求{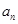 }的公比q;
}的公比q;
(2)若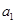 -
-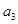 =3,求
=3,求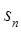 .
.
(本小题满分14分)
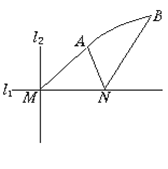
如图,直线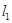 和
和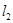 相交于点
相交于点 且
且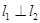 ,点
,点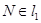 .以
.以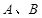 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到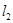 的距离与到点
的距离与到点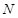 的距离相等.若
的距离相等.若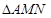 为锐角三角形,
为锐角三角形,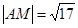 ,
,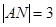 ,且
,且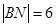 .
.
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点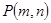 在曲线段C上,直线
在曲线段C上,直线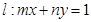 ,求直线
,求直线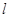 被圆
被圆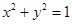 截得的弦长的取值范围.
截得的弦长的取值范围.