(本小题满分12分)
已知双曲线的方程为5x2-4y2=20,左右焦点分别为F1,F2
(1)求此双曲线的焦点坐标和渐近线方程;
(2)若椭圆与此双曲线有共同的焦点,且有一公共点P满足|PF1|·|PF2|=6,求椭圆的标准方程.
已知函数
(1)若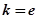 ,试确定函数
,试确定函数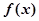 的单调区间;
的单调区间;
(2)若 且对任意
且对任意 ,
,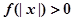 恒成立,试确定实数
恒成立,试确定实数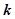 的取值范围;
的取值范围;
(3)设函数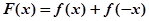 ,求证:
,求证: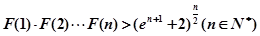
.已知椭圆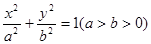 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足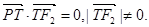

(Ⅰ)设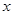 为点P的横坐标,证明
为点P的横坐标,证明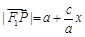 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1M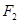 的面积S=
的面积S=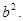 若存在,求∠F1MF2的正切值;若不存在,请说明理由.
若存在,求∠F1MF2的正切值;若不存在,请说明理由.
.已知函数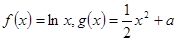 (
( 为常数),直线l与函数
为常数),直线l与函数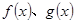 的图象都相切,且l与函数
的图象都相切,且l与函数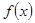 的图象的切点的横坐标为1.
的图象的切点的横坐标为1.
(1)求直线l的方程及a的值;(2)当k>0时,试讨论方程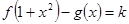 的解的个数.
的解的个数.
平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足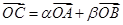 ,其中
,其中 ,且
,且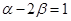
(1)求点C的轨迹方程;(2)设点C的轨迹与双曲线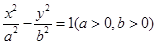 交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于
交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于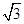 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
设正数数列 的前n次之和为
的前n次之和为 满足
满足 =
=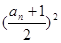
①求 ,
,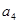 ②猜测数列
②猜测数列 的通项公式,并用数学归纳法加以证明
的通项公式,并用数学归纳法加以证明
③设 ,数列
,数列 的前n项和为
的前n项和为 ,求
,求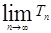 的值.
的值.