(本小题满分14分)已知椭圆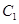 :
: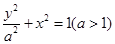 与抛物线
与抛物线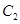 :
: 有相同焦点
有相同焦点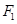 .
.
(Ⅰ)求椭圆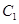 的标准方程;
的标准方程;
(Ⅱ)已知直线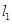 过椭圆
过椭圆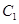 的另一焦点
的另一焦点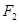 ,且与抛物线
,且与抛物线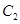 相切于第一象限的点
相切于第一象限的点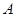 ,设平行
,设平行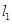 的直线
的直线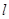 交椭圆
交椭圆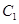 于
于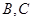 两点,当△
两点,当△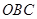 面积最大时,求直线
面积最大时,求直线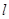 的方程.
的方程.
(本小题满分12分)如图1所示,在 中,
中, ,
, ,
, ,
, 为
为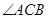 的平分线,点
的平分线,点 在线段
在线段 上,
上,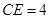 .如图2所示,将
.如图2所示,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,连结
,连结 ,设点
,设点 是
是 的中点.
的中点.
(1)求证: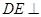 平面
平面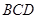 ;
;
(2)若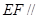 平面
平面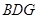 ,其中
,其中 为直线
为直线 与平面
与平面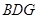 的交点,求三棱锥
的交点,求三棱锥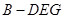 的体积.
的体积.
(本小题满分12分) 为了比较注射 两种药物后产生的皮肤疱疹的面积,选200只老鼠做试验,将这200只老鼠随机地分成两组,每组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只老鼠做试验,将这200只老鼠随机地分成两组,每组100只,其中一组注射药物 (称为
(称为 组),另一组注射药物
组),另一组注射药物 (称为
(称为 组),则
组),则 两组老鼠皮肤疱疹面积(单位:
两组老鼠皮肤疱疹面积(单位: )的频率分布表、频率分布直方图分别如下:
)的频率分布表、频率分布直方图分别如下: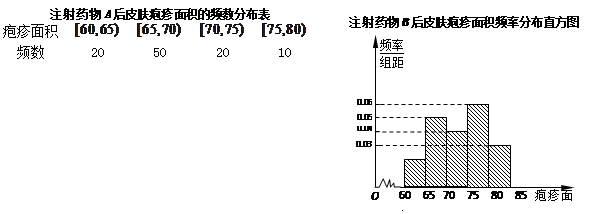
(1)为方便 两组试验对比,现都用分层抽样方法从
两组试验对比,现都用分层抽样方法从 两组中各挑出20只老鼠,求
两组中各挑出20只老鼠,求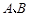 两组成肤疱疹面积同为
两组成肤疱疹面积同为 的这一区间应分别挑出几只?
的这一区间应分别挑出几只?
(2)在(Ⅰ)的条件下,将 两组挑出的皮肤疱疹面积同为
两组挑出的皮肤疱疹面积同为 这一区间上的老鼠放在一起观察,几天后,从中抽取两只抽血化验,求
这一区间上的老鼠放在一起观察,几天后,从中抽取两只抽血化验,求 组中至少有1只被抽中的概率.
组中至少有1只被抽中的概率.
(本小题满分12分) 在 中,角
中,角 对的边分别为
对的边分别为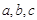 ,且
,且
(1)求 的值;
的值;
(2)若 ,求
,求 的面积
的面积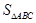 。
。
(本题满分13分)
已知直线 与椭圆
与椭圆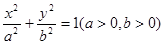 相交于A、B两点.
相交于A、B两点.
(Ⅰ)若椭圆的离心率为 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(Ⅱ)若向量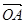 与向量
与向量 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率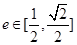 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值.
(本题满分14分)
已知函数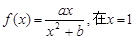 处取得极值为2.
处取得极值为2.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若函数 在区间
在区间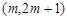 上为增函数,求实数m的取值范围;
上为增函数,求实数m的取值范围;
(Ⅲ)若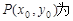
 图象上的任意一点,直线l与
图象上的任意一点,直线l与
 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.