我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例。如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了
（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律。例如，在三角形中第三行的三个数1，2，1，恰好对应
展开式中的系数;第四行的四个数1，3，3，1，恰好对应着
展开式中的系数等等。
（1）根据上面的规律，写出
的展开式。
（2）利用上面的规律计算：
作图题(不写作法,保留作图痕迹)（5分)
利用尺规过C点作与直线AB平行的直线PQ（不能用平推的方法作）.
在平面直角坐标系xOy中，已知抛物线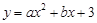
的对称轴是
，并且经过点（－2，－5）．
（1）求此抛物线的解析式；
（2）设此抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于C点，D是线段BC上一点（不与点B、C重合），若以B、O、D为顶点的三角形与△BAC相似，求点D的坐标；
（3）点P在y轴上，点M在此抛物线上，若要使以点P、M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标.
如图，已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．
（1）连接GD，求证：△ADG≌△ABE；
（2）连接FC，观察并猜测∠FCN的度数是否总保持不变，
若∠FCN的大小保持不变，请说明理由；
若∠FCN的大小发生改变，请举例说明；
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=－2x＋80.设这种产品每天的 销售利润为y (元).
(1)求y与x之间的函数关系式，自变量x的取值范围；
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
（参考关系：销售额＝售价×销量，利润＝销售额-成本）
如图，⊙O是△ABC的外接圆，CE是边AB上的高，且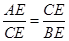
,CE的延长线交⊙O于点D．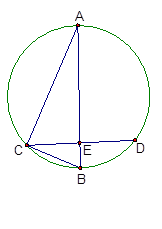
（1）求证：线段AB是⊙O的直径；
（2）若⊙O的半径为5，CD=8，求BE的长．