在平面直角坐标系中,已知 三个顶点的坐标分别为
三个顶点的坐标分别为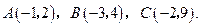
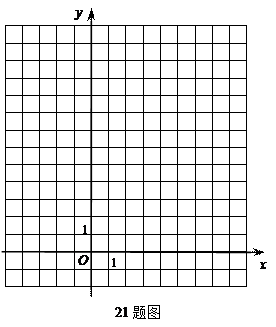
(1)画出 ,并求出
,并求出 所在直线的解析式。
所在直线的解析式。
(2)画出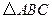 绕点
绕点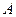 顺时针旋转
顺时针旋转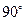 后得到的
后得到的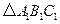 ,并求出
,并求出 在上述旋转过程中扫过的面积。
在上述旋转过程中扫过的面积。
已知:如图,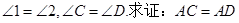

(1)计算:
(2)给出三个多项式:
请你选择其中两个进行加法运算,并把结果因式分解。
如图,对称轴为直线x=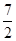 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.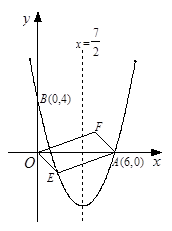
某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
| A |
B |
|
| 进价(元/件) |
1200 |
1000 |
| 售价(元/件) |
1380 |
1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
请你画出一个以BC为底边的等腰ΔABC,使底边上的高AD=BC.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.