(10分)如图1,O为正方形ABCD的中心,
分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转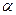 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当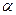 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.
计算(每小题6分,共18分):
24.(1)  (2)
(2) 
(3)化简求值: ,其中
,其中
如图所示,将矩形 沿
沿 折叠,使点
折叠,使点 恰好落在
恰好落在 上
上 处,以
处,以 为边作正方形
为边作正方形 ,延长
,延长 至
至 ,使
,使 ,再以
,再以 、
、 为边作矩形
为边作矩形 .
.
(1).试比较 、
、 的大小,并说明理由.
的大小,并说明理由.
(2).令 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由. 为定值.
为定值.
(3).在(2)的条件下,若 为
为 上一点且
上一点且 ,抛物线
,抛物线 经过
经过 、
、 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.
(4).在(3)的条件下,若抛物线 与线段
与线段 交于点
交于点 ,试问在直线
,试问在直线 上是否存在点
上是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求直线
相似?若存在,请求直线 与
与 轴的交点
轴的交点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知某种水果的批发单价与批发量的函数关系如图(1)所示.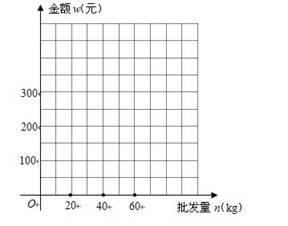
(1).请说明图中①、②两段函数图象的实际意义;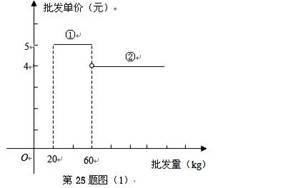
(2).写出批发该种水果的资金金额w(元)与批发量n(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
(3).经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.
2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.
(1).该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2).该市政府2009年投入“需方”和“供方”的资金各多少万元?
(3).该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年平均增长率.
已知:如图,在平面直角坐标系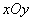 中,直线AB分别与
中,直线AB分别与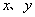 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,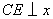 轴于点E,
轴于点E, .
.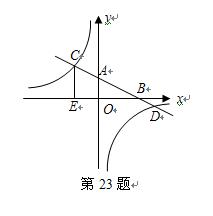
(1).求该反比例函数的解析式;
(2).求直线AB的解析式