如图,在平面直角坐标系中,直线 分别交
分别交 轴,
轴, 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点M从点A出发,沿线段AB以每秒 个单位长度的速度向终点B运动,过点P作
个单位长度的速度向终点B运动,过点P作 ,垂足为H,连接
,垂足为H,连接 ,
, .设点P的运动时间为
.设点P的运动时间为 秒.
秒.
①若△MPH与矩形AOCD重合部分的面积为1,求 的值;
的值;
②点Q是点B关于点A的对称点,问 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
小红想要测量校园内一座教学楼CD的高度.她先在A处测得楼顶C的仰角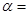 30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角
30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角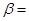 60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米)参考数据:
60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米)参考数据: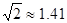 ,
,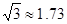 ,
,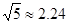
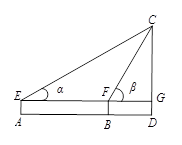
如图,在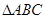 中,
中,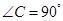 ,
,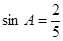 ,
,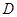 为
为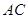 上一点,
上一点,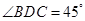 ,
,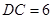 ,求
,求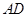 的长.
的长.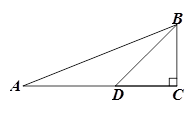
已知二次函数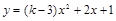 的图象与x轴有交点,求k的取值范围.
的图象与x轴有交点,求k的取值范围.
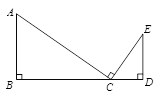
如图,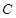 为线段
为线段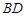 上一点,
上一点,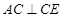 ,
,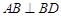 ,
,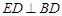 .求证:
.求证: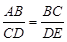 .
.
如图,有一边长为5的正方形ABCD和一等腰 PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线
PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线 上,当Q、C两点重合时,等腰
上,当Q、C两点重合时,等腰 PQR以每秒1cm的速度沿直线
PQR以每秒1cm的速度沿直线 按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰
按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰 PQR重叠部分的面积为S。
PQR重叠部分的面积为S。
(1)当t=3秒时,PQ与CD相交于点F,点E为QR的中点,连结PE,求证: QCF ∽
QCF ∽ QEP.
QEP.
(2)当t=5秒时,求S的值.
(3)当8≤t<9时,求S关于t的函数表达式.
(4)当9≤t≤13时,求S关于t的函数表达式.