如图,有一边长为5的正方形ABCD和一等腰 PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线
PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线 上,当Q、C两点重合时,等腰
上,当Q、C两点重合时,等腰 PQR以每秒1cm的速度沿直线
PQR以每秒1cm的速度沿直线 按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰
按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰 PQR重叠部分的面积为S。
PQR重叠部分的面积为S。
(1)当t=3秒时,PQ与CD相交于点F,点E为QR的中点,连结PE,求证: QCF ∽
QCF ∽ QEP.
QEP.
(2)当t=5秒时,求S的值.
(3)当8≤t<9时,求S关于t的函数表达式.
(4)当9≤t≤13时,求S关于t的函数表达式.
(本小题满分14分)根据下列要求,解答相关问题.
(1)请补全以下求不等式 的解集的过程.
的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数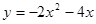 ;并在下面的坐标系中(见图1)画出二次函数
;并在下面的坐标系中(见图1)画出二次函数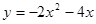 的图象(只画出图象即可).
的图象(只画出图象即可).
②求得界点,标示所需:当y=0时,求得方程 的解为;并用锯齿线标示出函数
的解为;并用锯齿线标示出函数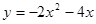 图象中y≥0的部分.
图象中y≥0的部分.
③借助图象,写出解集:由所标示图象,可得不等式 的解集为.
的解集为.
(2)利用(1)中求不等式解集的步骤,求不等式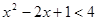 的解集.
的解集.
①构造函数,画出图象:
②求得界点,标示所需:
③借助图像,写出解集:
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式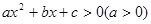 的解集.
的解集.

(本小题满分10分)如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F.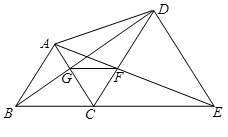
求证:(1)△ACE≌△BCD;
(2) .
.
(本小题满分10分)一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件.为提高利润,欲对该T恤进行涨价销售.经过调查发现:每涨价1元,每周要少卖出10件.请确定该T恤涨价后每周的销售利润y(元)与销售单价x(元)之间的函数关系式,并求销售单价定为多少元时,每周的销售利润最大?
(本小题满分9分)如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
(1)求弧BC的长;
(2)求弦BD的长.
(本小题满分9分)根据要求,解答下列问题.
(1)解下列方程组(直接写出方程组的解即可):
①
 .
.
②
 .
.
③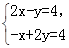
 .
.
(2)以上每个方程组的解中,x值与y值的大小关系为.
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.