（本小题满分14分）根据下列要求，解答相关问题.
（1）请补全以下求不等式
的解集的过程.
①构造函数，画出图象：根据不等式特征构造二次函数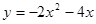
；并在下面的坐标系中(见图1)画出二次函数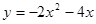的图象（只画出图象即可）.
②求得界点，标示所需：当y=0时，求得方程
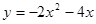的解为 ；并用锯齿线标示出函数图象中y≥0的部分.
③借助图象，写出解集：由所标示图象，可得不等式的解集为 .
（2）利用（1）中求不等式解集的步骤，求不等式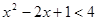
的解集.
①构造函数，画出图象：
②求得界点，标示所需：
③借助图像，写出解集：
（3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式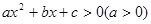
的解集.
已知m是方程x2-x-2=0的一个实数根，求代数式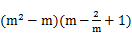
的值.
已知：如图，在Rt△ABC中，∠C=90°，∠BAD=
∠BAC，过点D作DE⊥AB，DE恰好是∠ADB的平分线，求证：CD=DB.
有一批图形计算器，原售价为每台800元，在甲、乙两家公司销售．甲公司用如下方法促销：买一台单价为780元，买两台每台都为760元．依次类推，即每多买一台，则所买各台单价均再减20元，但最低不能低于每台440元；乙公司一律按原售价的75%促销．某单位需购买一批图形计算器：
（1）若此单位需购买6台图形计算器，应去哪家公司购买花费较少？
（2）若此单位恰好花费7 500元，在同一家公司购买了一定数量的图形计算器，请问是在哪家公司购买的，数量是多少？
如图，一次函数y＝kx＋b与反比例函数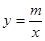
的图象交于A（2，3），B（－3，n）两点．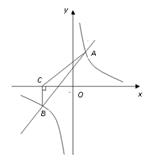
（1）求一次函数与反比例函数的解析式；
（2）根据所给条件，请直接写出不等式kx＋b＞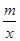
的解集______________；
（3）过点B作BC⊥x轴，垂足为C，求S△ABC．
某池塘里养了鱼苗1万条，根据这几年的经验知道，鱼苗成活率为95%，一段时间后准备打捞出售，第一网捞出40条，称得平均每条鱼重2.5千克，第二网捞出25条，称得平均每条鱼重2.2千克，第三网捞出35条，称得平均每条鱼重2.8千克，试估计这池塘中鱼的质量.