一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出1个球,记录下颜色后放回袋中并搅匀,再从中任意摸出1个球。请用画树状图的方法列出所有可能的结果,并写出两次摸出的球颜色相同的概率。
直线AB、CD被直线EF所截,EF分别交AB、CD于M,N,∠EMB=50°,

MG平分∠BMF,MG交CD于G.
(1)如图1,若AB∥CD,求∠1的度数.
(2)如图2,若∠MNC=140°,求∠1的度数.
政府引导农民对生产的土特产进行加工后,分为甲、乙、丙三种不同包装
推向市场进行销售,其相关信息如下表:
| 重量(克/袋) |
销售价(元/袋) |
成本(元/袋) |
|
| 甲 |
400 |
4.8 |
3.8 |
| 乙 |
300 |
3.6 |
2.9 |
| 丙 |
200 |
2.5 |
1.9 |
这三种不同的包装的土特产都销售了120千克,那么本次销售中,那一种包装的
土特产获得的利润最大,最大利润是多少?
如图,∠B=55°,∠EAC=110°,AD平分∠EAC,AD与BC平行吗?为什么?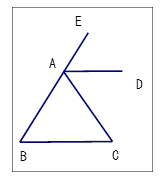
根据下面的解答过程,在括号内填空或填写理由.
解:∵AD平分∠EAC,∠EAC=110°(已知)
∴ EAD=
EAD=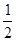
 EAC=°
EAC=°
∵ B=55°(已知)
B=55°(已知)
∴ B=
B= ()
()
∴AD∥BC()
.某校为了解该校学生的课余活动情况,从阅读、运动、娱乐、其它四个方面
调查了若干名学生的爱好,经统计整理,绘制成不完整的扇形统计图与条形统计图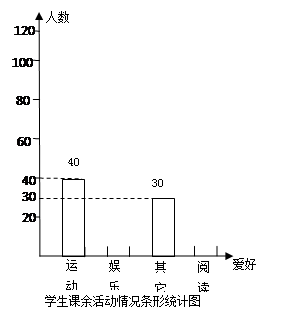 如下,请回答如下问题:
如下,请回答如下问题:
(1)本次共调查了多少人?
(2)把条形统计图补充完整;
(3)求其它所在扇形的圆心角的度数.
 |

已知线段AB,在方格纸上画出以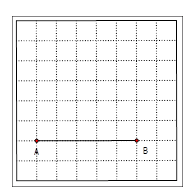
下图形.
(1) 画∠ABC=45º;
(2) 在(1)的条件下,过点A画AD⊥BC,
垂足为D.