两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?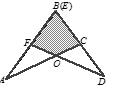
有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法,表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线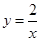 上的概率.
上的概率.
如图,在△ABC中,AC⊥BC,D是BC延长线上的一点,E是AC上的一点,连接ED,∠A=∠D.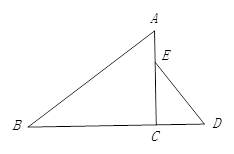
(1)求证:△ABC∽△DEC;
(2)若AC=3,AE=1,BC=4,求DE的长.
如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取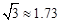 ,结果保留整数)
,结果保留整数)
在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,求木竿PQ的长度。
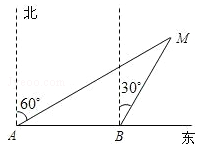
如图所示,某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M 在北偏东30°方向处,问B处到灯塔M的距离是多少海里?