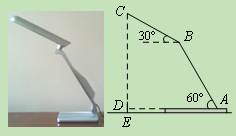
如图，放置在水平桌面上的台灯的灯臂AB长为40cm，灯
罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠BAD="60°." 使用发现，光线最
佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？
如图，A、D、B、C是⊙O上的四点，∠ADC=∠CDB=60°，判断△ABC的形状并证明你的结论。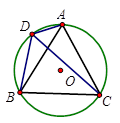
已知二次函数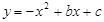
的图象如图所示，它与x轴的一个交点坐标为（－1，0），与y轴的交点坐标为（0，3）。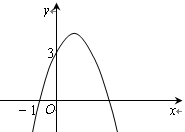
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围。
如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A（1，3）、B（2，2）、C（2，1），D（3，3）．
（1）以原点O为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；
（2）在（1）的前提下，写出点A的对应点坐标A′．
如图，在平面直角坐标系中，A（a，0），B（b，0），C（-2，1），且|a+2b＋1|+(3a-4b+13)2＝0．
（1）求a，b的值；
（2）在y轴上存在一点D，使得△COD的面积是△ABC面积的两倍，求出点D的坐标．
（3）在x轴上是否存在这样的点，存在请直接写出点D的坐标，不存在请说明理由．
七（1）班同学为了解2013年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，
| 月均用水量 x(t) |
频数(户) |
百分比 |
| 0<x≤5 |
6 |
12% |
| 5<x≤10 |
24% |
|
| 10<x≤15 |
32% |
|
| 15<x≤20 |
10 |
20% |
| 20<x≤25 |
4 |
|
| 25<x≤30 |
2 |
4% |
请解答以下问题：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）求该小区用水量不超过15t的家庭占被调查家庭总数的百分比；
（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20t的家庭大约有多少户？