如图,在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,3)、B(2,2)、C(2,1),D(3,3).
(1)以原点O为位似中心,相似比为2,将图形放大,画出符合要求的位似四边形;
(2)在(1)的前提下,写出点A的对应点坐标A′.
有一组等式: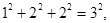
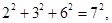
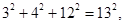
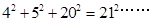 请观察它们的构成规律,用你发现的规律解答下面的问题:
请观察它们的构成规律,用你发现的规律解答下面的问题:
(1)写出第8个等式为;
(2)试用含正整数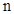 的等式表示你所发现的规律;
的等式表示你所发现的规律;
(3)说明你在(2)中所写等式成立的理由.
(1)已知(a-b)2=15,(a+b)2=7,计算ab的值;
(2)阅读理解:已知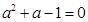 ,求
,求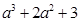 的值.
的值.
解: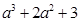
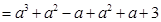
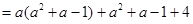
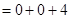
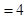
请你参照以上方法解答下面问题:
如果 ,试求代数式
,试求代数式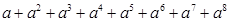 的值
的值
在正方形网格中,每个小正方形的边长均为1个单位长度,△ 的三个顶点的位置如图所示,现将△
的三个顶点的位置如图所示,现将△ 平移,使点
平移,使点 对应点
对应点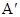 ,点
,点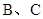 分别对应点
分别对应点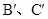 .
.
(1) 画出平移后的△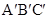 .
.
(2) △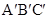 的面积是_;
的面积是_;
(3) 连接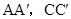 ,则这两条线段之间的关系是____.
,则这两条线段之间的关系是____.
如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC,于D,求∠ABD的度数.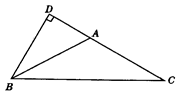
已知|a-b-1|与(b-2014)2互为相反数,求代数式a2-2ab+b2的值.