甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量 (件)与时间
(件)与时间 (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.
已知:如图,在Rt△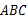 中,∠
中,∠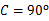 ,点
,点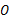 在
在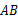 上,以
上,以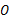 为圆心,
为圆心,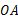 长为半径的圆与
长为半径的圆与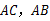 分别交于点
分别交于点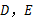 ,且∠
,且∠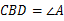 .判断直线
.判断直线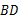 与
与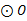 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.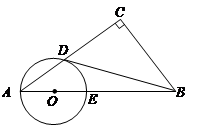
如图,△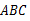 内接于
内接于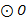 ,∠
,∠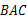 =
=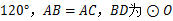 的直径,
的直径,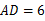 ,求
,求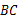 的长.
的长.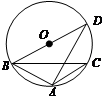
已知下列n(n为正整数)个关于x的一元二次方程: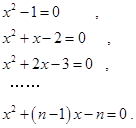
(1)请解上述一元二次方程;
(2)请你指出这n个方程的根具有什么共同特点,写出一条即可.
某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2 000万元,2010年投入的资金是2 420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?