如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从
点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C
两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设
点P的运动时间为x(秒).
(1)用含有x的代数式表示CF的长.
(2)求点F与点B重合时x的值.
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.
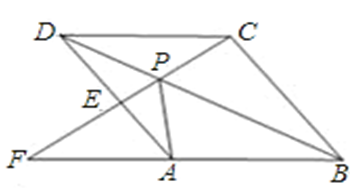
如图,点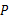 是菱形
是菱形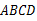 的对角线
的对角线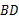 上一点,连接
上一点,连接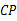 并延长,交
并延长,交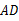 于
于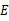 ,交
,交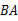 的延长线于点
的延长线于点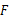 .
.
(1)图中△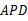 与哪个三角形全等?并说明理由.
与哪个三角形全等?并说明理由.
(2)求证:△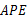 ∽△
∽△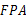 .
.
(3)猜想:线段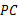 ,
,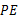 ,
,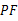 之间存在什么关系?并说明理由.
之间存在什么关系?并说明理由.
已知关于 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
.
(1)求实数 的取值范围;
的取值范围;
(2)当 时,求
时,求 的值.
的值.
如图,在等腰梯形 中,
中, ∥
∥ ,点
,点 是线段
是线段 上的一个动点(
上的一个动点( 与
与 、
、 不重
不重
合), 分别是
分别是 的中点.
的中点.
(1)试探索四边形 的形状,并说明理由.
的形状,并说明理由.
(2)当点 运动到什么位置时,四边形
运动到什么位置时,四边形 是菱形?并加以证明.
是菱形?并加以证明.
(3)若(2)中的菱形 是正方形,请探索线段
是正方形,请探索线段 与线段
与线段 的关系,并证明你的结论.
的关系,并证明你的结论.
如图,在等腰梯形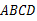 中,
中, ∥
∥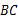 ,
, 分别是
分别是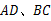 的中点,
的中点,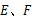 分别是
分别是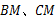 的中点.
的中点.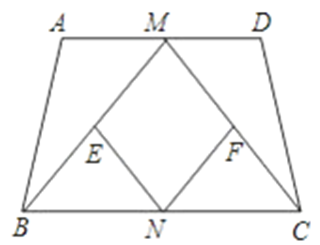
(1)求证:四边形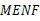 是菱形;
是菱形;
(2)若四边形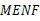 是正方形,请探索等腰梯形
是正方形,请探索等腰梯形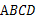 的高和底边
的高和底边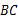 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
如图,点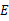 是正方形
是正方形 内一点,△
内一点,△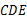 是等边三角形,连接
是等边三角形,连接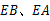 ,延长
,延长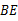 交边
交边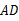 于点
于点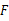 .
.
(1)求证:△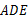 ≌△
≌△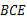 ;(2)求∠
;(2)求∠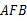 的度数.
的度数.