(本题9分)如图,△ABC是直角三角形,∠ACB=90°.
(1)实践与操作利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作△ABC的外接圆,圆心为O;
②以线段AC为一边,在AC的右侧作等边△ACD;
③连接BD,交⊙O于点F,连接AE,
(2)综合与运用 在你所作的图中,若AB=4,BC=2,则:
①AD与⊙O的位置关系是______.(2分)
②线段AE的长为__________.(2分)
(本小题满分10分) △ABC中,AC=BC.以BC为直径作⊙O交AB于点D,交AC于点G.直线DF⊥AC,垂足为F,交CB的延长线于点E.
△ABC中,AC=BC.以BC为直径作⊙O交AB于点D,交AC于点G.直线DF⊥AC,垂足为F,交CB的延长线于点E.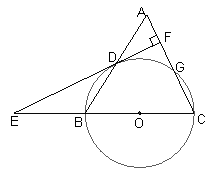
(1)判断直线EF与⊙O的位置关系,并
 说明理由;
说明理由;(2)如果BC=10,AB=12,求CG的长.
(本小题满分10分)
在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是: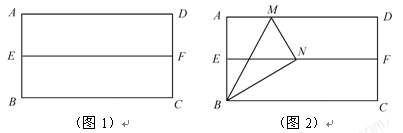
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2)
请解答以下问题:(1)如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论.
(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?
(本小题满分12分)
如图,反比例函数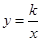 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题: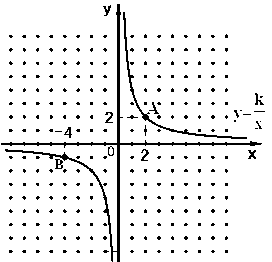
(1)写出A点的坐标;
(2)求反比例函数的解析式;
(3)若点A绕坐标原点O旋转90°后得到点C,请写出点C的坐标;并求出直线BC的解析式.
(本小题满分10分)
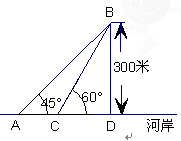
如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?(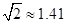 ,
,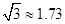 )
)
(本题满分10分第(1)小题满分4分,第(2)小题满分3分,第(3)小题满分3分)
某中学对全校学生60秒跳绳的次数进行了统计,全校平均次数是100次.某班体育委员统计了全班40名学生60 秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么
秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么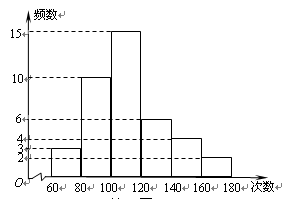
(1)该班60秒跳绳的平均次数至少是 ▲.
(2)该班学生跳绳成绩的中位数所在范围是 ▲.
(3)从该班中任选一人,其跳绳次数达到或超过校平均次数的概率是 ▲.