某校宣传栏中公示了担任下学期七年级班主任的12位老师的情况(见下表),小凤准备到该校就读七年级,请根据表中信息帮小凤进行如下统计分析:
| 姓名 |
性别 |
年龄 |
学历 |
职称 |
姓名 |
性别 |
年龄 |
学历 |
职称 |
|
| 王雄辉 |
男 |
35 |
本科 |
高级 |
蔡 波 |
男 |
45 |
大专 |
高级 |
|
| 李 红 |
男 |
40 |
本科 |
中级 |
李 凤 |
女 |
27 |
本科 |
初级 |
|
| 刘梅英 |
女 |
40 |
中专 |
中级 |
孙 焰 |
男 |
40 |
大专 |
中级 |
|
| 张 英 |
女 |
43 |
大专 |
高级 |
彭朝阳 |
男 |
30 |
大专 |
初级 |
|
| 刘 元 |
男 |
50 |
中专 |
中级 |
龙 妍 |
女 |
25 |
本科 |
初级 |
|
| 袁 桂 |
男 |
30 |
本科 |
初级 |
杨 书 |
男 |
40 |
本科 |
中级 |
(1)该校下学期七年级班主任老师年龄的众数是多少?
(2)在图7(1)中,将反映老师学历情况的条形统计图补充完整;
(3)在图7(2)中,标注扇形统计图中表示老师职称为初级和高级的百分比;
(4)小凤到该校就读七年级,班主任老师是女老师的概率是多少?

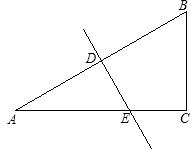
已知:如图,AB=AE,BC=ED,AF⊥CD且F是CD的中点,
求证:∠B=∠E.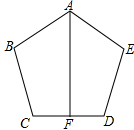
如图,在△ABC中,∠A=90°,DE垂直平分线段BC,分别交AC、BC于点D、E,BD平分∠ABC.
(1)直接写出图中相等的线段.(写出三组,即可得满分)
(2)试判断∠ABD与∠C的大小关系,并证明你的判断结论.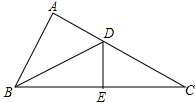
如图,直线l是线段AB的中垂线,P点在直线l的右侧,则点P到A、B的距离有何关系?请写出你的结论,并说明理由.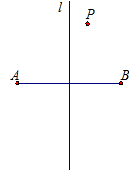
如图,已知DE是△ABC的边AB的垂直平分线交AB于D,BC于E,AE恰好是∠BAC的平分线,若∠B=30°.
(1)求∠C的度数;
(2)你发现了什么?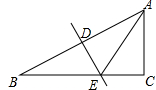
已知:如图,△ABC中,∠C=90°,∠A=30°,ED垂直平分AB交AB于D,交AC于E.求证:ED=EC.