(本小题满分14分)设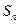 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 N
N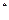 ,都有
,都有
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比 ,数列
,数列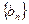 满足
满足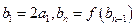
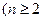 ,
, N
N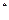
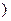 ,求数列
,求数列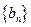 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求证:数列 的前
的前 项和
项和 .
.
在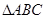 中,角
中,角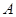 、
、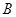 、
、 的对边分别为
的对边分别为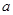 、
、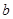 、
、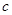 ,
,
且满足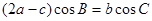 .
.
(1)求角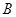 的大小;
的大小;
(2)当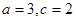 时,求
时,求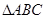 的面积
的面积
已知函数
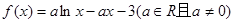

 .
.
(Ⅰ)求函数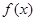 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点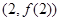 处的切线的斜率为
处的切线的斜率为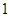 ,问:
,问:  在什么范围取值时,对于任意的
在什么范围取值时,对于任意的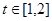 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数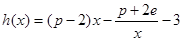 ,若在区间
,若在区间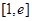 上至少存在一个
上至少存在一个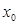 ,使得
,使得 成立,试求实数
成立,试求实数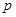 的取值范围.
的取值范围.
已知函数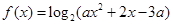 ,
,
(Ⅰ)当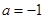 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;
(Ⅱ)如果 在区间
在区间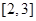 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围
如图,四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为梯形,
为梯形, ,
,
 ,且
,且 ,点
,点 是棱
是棱 上的动点.
上的动点.
(Ⅰ)当 ∥平面
∥平面 时,确定点
时,确定点 在棱
在棱 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角 的余弦值.
的余弦值.
在 中,
中, 分别为角
分别为角
 所对的边,且
所对的边,且 ,
,
(Ⅰ)求角 ;
;
(Ⅱ)若 ,
,
 ,
, 的周长为
的周长为 ,求函数
,求函数 的取值范围.
的取值范围.