（11·漳州）（满分14分）如图1，抛物线y＝mx2－11mx＋24m (m＜0) 与x轴交于B、C两点（点B在点C的左侧），抛物线另有一点A在第一象限内，且∠BAC＝90°．
（1）填空：OB＝_ ▲ ，OC＝_ ▲ ；
（2）连接OA，将△OAC沿x轴翻折后得△ODC，当四边形OACD是菱形时，求此时抛物线的解析式；
（3）如图2，设垂直于x轴的直线l：x＝n与（2）中所求的抛物线交于点M，与CD交于点N，若直线l沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．
如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC＝BD.求证: (1)BC＝AD; (2)△OAB是等腰三角形.
如图，D是△ABC边BC上的一点，且DA平分∠EDC，∠E=∠B，ED=DC，求证：AB=AC．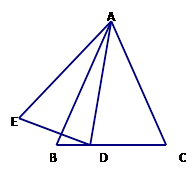
如图，小明在完成数学作业时，遇到了这样一个问题，AB=CD，AD=BC，请说明∠B=∠D的道理，小明动手测量了一下，发现∠B确实与∠D相等，但他不能说明其中的道理，你能帮助他说明这个道理吗？试试看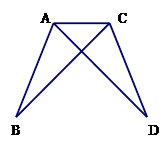
作图题：(5′+5′+5′，共15分)
（1）如图，已知∠AOB及点C、D两点，请利用直尺和圆规作一点P，使得点P到射线OA、OB的距离相等，且P点到点C、D的距离也相等。
（2）利用方格纸画出△ABC关于直线
的对称图形△A′B′C′。
（3）如图，已知在△ABC中，AB="AC" ，AD是BC边上的高，P是AB边上的一点，试在高AD上找一点E，使得△PEB的周长最短。
在数1，2，3，…，1998前添符号“+”和“-”，并依次运算，所得可能的最小非负数是多少？