作图题：(5′+5′+5′，共15分)
（1）如图，已知∠AOB及点C、D两点，请利用直尺和圆规作一点P，使得点P到射线OA、OB的距离相等，且P点到点C、D的距离也相等。
（2）利用方格纸画出△ABC关于直线
的对称图形△A′B′C′。
（3）如图，已知在△ABC中，AB="AC" ，AD是BC边上的高，P是AB边上的一点，试在高AD上找一点E，使得△PEB的周长最短。
吸烟有害健康！你知道吗，即使被动吸烟也大大危害健康．
有消息称，我国准备从2011年元月一日起在公众场所实行“禁烟”，为配合“禁烟”行动，某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查，征求市民的意见，并将调查结果整理后制成了如下统计图：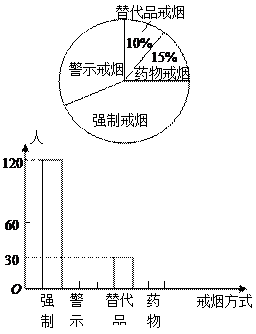
根据统计图解答：
（1）同学们一共随机调查了多少人？
（2）请你把统计图补充完整；
（3）如果在该社区随机咨询一位市民，那么该市民支持“强制戒烟”的概率是多少？假定该
社区有1万人，请估计该地区大约有多少人支持“警示戒烟”这种方式．
求代数式的值：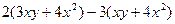
其中
解方程：
计算：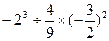
如图，已知线段
与
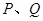两点，
① 过P点画出线段的垂线
；
② 过Q点画出线段的平行线
；
③ 则有
.
（在横线上填入适当的数学符号，保留作图痕迹，不写画法）