（11·漳州）（满分14分）如图1，抛物线y＝mx2－11mx＋24m (m＜0) 与x轴交于B、C两点（点B在点C的左侧），抛物线另有一点A在第一象限内，且∠BAC＝90°．
（1）填空：OB＝_ ▲ ，OC＝_ ▲ ；
（2）连接OA，将△OAC沿x轴翻折后得△ODC，当四边形OACD是菱形时，求此时抛物线的解析式；
（3）如图2，设垂直于x轴的直线l：x＝n与（2）中所求的抛物线交于点M，与CD交于点N，若直线l沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．
如图所示，一幢楼房AB背后有一台阶CD，台阶每层高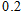
米，且AC=
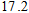米，设太阳光线与水平地面的夹角为
.当
时，测得楼房在地面上的影长AE=
米，现有一只小猫睡在台阶的MN这层上晒太阳.（
取
）
（1）求楼房的高度约为多少米？
（2）过了一会儿，当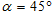
时，问小猫能否还晒到太阳？请说明理由.
已知：如图，AB∥CD，E是AB的中点，CE＝DE．
求证：（1）∠AEC＝∠BED；（2）AC＝BD．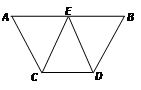
如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）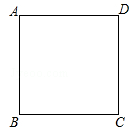
如图，轮船甲位于码头O的正西方向A处，轮船乙位于码头O的正北方向C处，测得∠CAO=45°，轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为45km/h和36km/h，经过0.1h，轮船甲行驶至B处，轮船乙行驶至D处，测得∠DBO=58°，此时B处距离码头O多远？（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1，60）
如图，△ABC中，CD是边AB上的高，且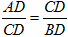
．
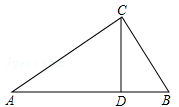
（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．