如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1
和△A2B2C2：
(1)将△ABC先向右平移4个单位，再向上平移1个单位，得到△A1B1C1；
(2)以图中的点O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2．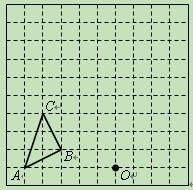
化简：（1）
；
（2）
计算：（1）18－6÷(－3)×2
（2）
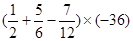
（3）
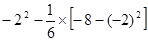
如图(1)，在梯形ABCD中，AD∥BC，且AD＝4cm，AB＝6cm，BC=12cm，DC＝10cm.若动点P从A点出发，以每秒4cm的速度沿线段AD、DC向C点运动；动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时，动点P、Q同时停止运动. 设点P、Q同时出发，并运动了t秒.
（1）求梯形ABCD的面积.
（2）当t为何值时，四边形PQCD成为平行四边形？
（3）是否存在t，使得P点在线段DC上，且PQ⊥DC（如图(2)所示）？若存在，求出此时t的值，若不存在，说明理由.
如图，点O是等边△ABC内一点，∠AOB=110º，∠BOC=
,将△BOC绕点C按顺时针方向旋转60º得△ADC，连接OD．
（1）△COD是什么三角形？说明理由；
（2）若AO=
，AD=
,OD=
(
为大于1的整数)，求的度数；
（3）当为多少度时，△AOD是等腰三角形？ 
如图，△ABC中，AD是边BC上的高，CF是边AB上的中线，且DC＝BF，DE⊥CF于E.
（1）E是CF的中点吗？试说明理由；
（2）试说明：∠B＝2∠BCF.