如图(1),在梯形ABCD中,AD∥BC,且AD=4cm,AB=6cm,BC=12cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时,动点P、Q同时停止运动. 设点P、Q同时出发,并运动了t秒.
(1)求梯形ABCD的面积.
(2)当t为何值时,四边形PQCD成为平行四边形?
(3)是否存在t,使得P点在线段DC上,且PQ⊥DC(如图(2)所示)?若存在,求出此时t的值,若不存在,说明理由.
(本题共2个小题,每题5分,共10分)
(1)计算:
(2)解方程:
如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°。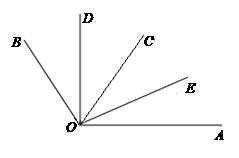
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由。
惠民超市第一天以每件10元的价格购进某品牌茶杯15个,由于此种品牌商品价格看涨,第二天又以每件12元的价格购进同种茶杯35个,然后以相同的价格卖出,商店在销售这些茶杯时,要想利润率不低于10%,你觉得该如何定价?
已知线段AB的长度为4cm,延长线段AB到C,使得BC=2AB,D是AC的中点,求BD的长。
如图,O为直线AB上一点,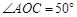 ,OD平分
,OD平分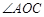 ,
, 。
。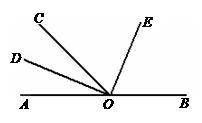
(1)请你数一数,图中有多少个小于平角的角;
(2)求出 的度数;
的度数;
(3)请通过计算说明OE是否平分 。
。