我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对
该特产的销售投资收益为:每投入x万元,可获得利润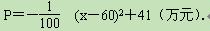
当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,
可获利润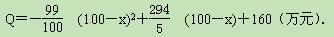
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.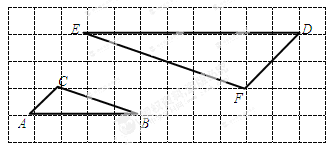
某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).
问:(1)当购买乒乓球多少盒时,两种优惠办法付款一样?
(2)当购买30盒乒乓球时,若让你选择一家商店去办这件事,你打算去哪家商店购 买?为什么?
如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.求:∠COE的度数.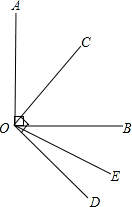
如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若ED=9,求线段AB的长度.
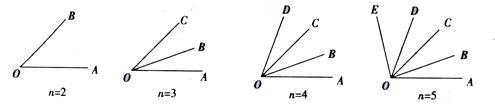
如图所示,从一点O出发,引两条射线可以得到一个角,引三条射线可以得到三个角,引四条射线可以得到六个角,引五条射线可以得到十个角,如果从一点出发引n(n为大于等于2的整数)条射线,则会得到多少个角?如果n=8时,检验你所得的结论是否正确。